Home > Steve > Puzzles > Teleports | Calendar Jigsaws
As I come across puzzles or recreational maths that I find interesting, I'll post them here. Generally I'll post answers embedded in the source of this page in comments.
At present there is:
Imagine that you have a very large garden and you want to plant trees to screen your garden from passers by, but that you still want to be freely able to wander around all of the garden.
You could achieve the desired effect by planting groups of trees well spaced out, for example you could plant a row with alternating 2m of shrubbery and then 2m of gap. Obviously this could been seen through, so you could plant another row, just the same 2m away from the first row. And a third row 2m from that. Etc.
If we imagine that each row is an infinitely long, infinitely thin 50% mark/space ratio "fence", How many rows and what positons do the rows need to be to make the combined effect opaque. (Ignore diffraction - light travels in straight lines here!)
If you don't understand the problem, an
example diagram of a failing three fence system should clarify
matters and may also provide a hint to the answer. The yellow is the
"line of sight" from the gap with the semi-circle. The grey is
the bits you can't see from that gap.
Don't forget to consider the infinite number of acute angles that are
involved.
Can you determine the following sequence and what are its next few terms?.
You have two irregular thickness ropes, Made irregular to stop you doing anything with "lengths". Despite this, it is known that if you set fire to either rope it will burn for exactly 1 hour.
How do you measure 3/4 hour? No tricks - a logical answer exists.
This is an extension of the opaque fences problem.
Assume that rain falls in straight lines, but angled at any direction due to the wind. If you have a house where you want to let smoke out easily but no rain in how many are needed and how do you place equi-spaced infinite "chess-board" roof layers to achieve this. (The black squares are solid roof tiles, the white squares are free space, and presumably there is some form of guttering at the corners of the squares to remove the water!)
I have no answer at present. :-(
Imagine an equilateral tetrahedron (four equilateral triangles assembled to make a triangular based pyramid).
For reasons inexplicable, 3 spiders and a fly are only able to walk along the edges of the tetrahedron. The spiders have to say where they start and exactly where they are going to walk in advance. The 'invisible' fly is clever and must be told their plans in advance so he can decide his starting point and movement.
The fly is ever so slightly slower than the spiders (say 99% of the speed), but being invisible, a spider only knows he has caught the fly by treading on it.
Can the spiders catch the fly? If so demonstrate how. Or can the fly forever remain uncaught? If so prove it.
I was sent this puzzle by email and had to be told the answer.
If there was only one spider, how much faster than the fly would he need to be to be able to catch it? If it was a thousand times faster it is easy to catch the fly, unless the fly is considered as a point object. How about 100 times or 10 times or 3.14159 times faster? Prove your value is the minimum required.
When this was planted it was the longest hedge maze in the world. If
you do it without a map - as 99% of folk do - you are unlikely to solve
it in under 2 hours. In summer carrying liquid is recommended.
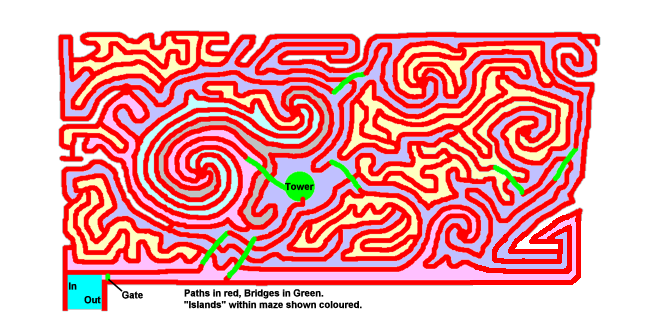
The maze has changed subtly over the years. The entrance (bottom left) was altered, extra hedges were grown in the bottom right to fill the corner out, the central tower access was changed from a path to a bridge and a quick exit bridge was provided. All these make previously published maps and aerial photos inaccurate. To the best of my knowledge, this is accurate as of 2006-10-09.
This puzzle was posted on Wikipedia's mathmatics reference desk by "Black Carrot". I found it interesting, so I'm presenting it here.
You have 25 horses, and a track on which you can race five of them at a time. You can determine in what order the horses in a race finished, but not how long they took, and so can not compare times from one race to another. A given horse runs at the same speed under all circumstances, and no two horses run at the same speed. How many races does it take to find the three fastest?
Home >
Steve >
Puzzles >
Teleports
Last updated 2022-04-20
This page is part of http://www.stocton.org/
Email: webmaster@stocton.org