Home > Steve > Go > Problem of the month

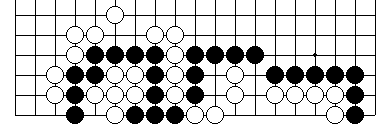
Black to play and live his group on the left or kill the White group on the right (or both).
If Black gets a choice of 'live on left' or 'rampage on right' but not both, which is bigger?
(Problem comes from a Japanese book which I can't read!)
In some ways this is a trick question, because it is hard to imaging
how black could kill the white group on the right without living his
black group on the left.
Presumably the only way would be for some capturing race to be involved,
but I am not aware of this being possible.
Do note that on the left, the white stones form a rabbity-six big-eye shape, therefore the black stones have lots of liberties - about 12 on the inside.
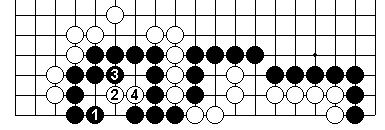
Black on the left is one-eyed and thus dead unless he manages to connect out.
This sequence would be sente if these moves kept Black dead, but as we shall see, he can connect out. Because of this White would treat 1 & 3 as gote, which means they are not even valid ko threats.
It would appear from these three diagrams that he can. And if he can then Black has no problem living...
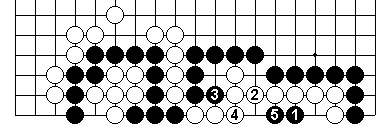
In this diagram White dies with his eyespace forced to one eye.
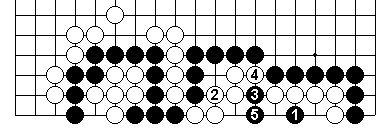
White dies from shortage of liberties, he can't atari from either side yet Black can.
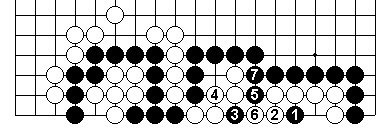
White second eye gets falsified here.
...But it turns out that there is a move which works for White.
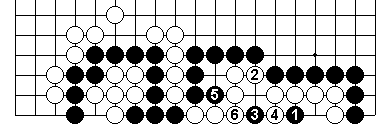
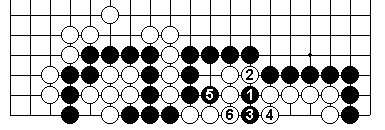
This is a futile attack, as are Black 1 at 1, 3, 4 or 5.
So how does Black live?
By connecting out.
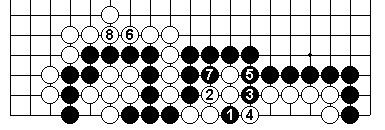
This is the right Black attack to which White has responded
"naturally" and as a result White has failed miserably.
(Black 9 at 1.)
 7 at 1
7 at 1
So White must give way to the Black 1 with White 2, and must then
save his group making two eyes with 6.
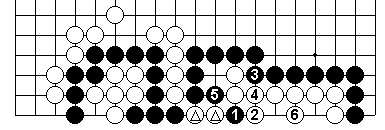
This Black threat to White's eye-space gives Black time to capture the
two triangled white stones with Black 7, thus linking his big one-eyed
left-hand group out.
Home >
Steve >
Go >
Problem of the month
British Go Association
Last updated 2004-08-10
This page is part of http://www.stocton.org/
Email: webmaster@stocton.org