Home > Steve > Go > Problem of the month

August 2000's Go Answer of the Month

In Go World 84, on page 59, there are a series of "Throw-in tesuji" problems.

Problem 5 seems to me more interesting if one of the failure answers is investigated.

Dia 1 - Failure diagram, Black 3 is an unimaginative move.

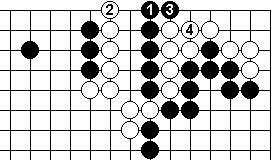
I paraphrase Go World: "After the exchange of Black 1 for White 2, Black 3 is an unimaginative move. White can connect with 4, so the six black stones will be captured."

This month's problem is to investigate this statement, to either kill the six black stones or to demonstrate that they cannot be killed.

Dia 2 - A likely candidate for Black 5.

After the sequence in Dia 1 it is Black's turn to play, and since the 'book' suggests that Black's cause is hopeless let's give Black the benefit of the next move. 5 here seems plausible: it removes a liberty from white and reduces the space available in the corner.

After 5, White has to play at one of the three marked points to protect the cutting point. With any other play, Black plays at the middle and removes the white group on the next move. We can consider this to be a Black success.

Lastly note that I am endeavouring to demonstrate that Black can kill White. To that end, this and the following diagrams will have White 2 from Dia 1 at A here. This reduces Black's liberties by one and makes it harder for him to succeed.

Dia 3 - White connects.

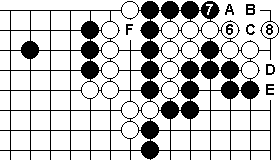
If White 6 connects, then both groups have 5 liberties, so Black has to play a white liberty. 7 seems as good as any.

I've been through most White 8's and this seems the strongest of them all.

• If White plays 8' at A, Black plays 9' at D and wins a straight-forward semeai.
• If 8' at B then 9' at the other 2-1 point and again wins the semeai.
• 8' at C and 9' at D suffices.
• 8' at D gets 9' at the right 2-1 point.
• 8' at E is harder. 9' throws in at D. Should White try extending from 8'(E), Black just plays solidly to keep White down to one liberty. When White eventually captures 9', Black pushes along the top and wins the race again.
• 8' at F requires Black 9' to jump to B. Eventually White will either fill in his own liberties or permit Black to connect gaining a liberty. Black wins this too.

Dia 4 - Black wins the race by one liberty.

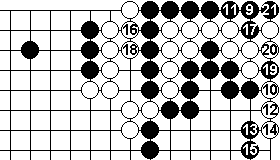
Other plays by White for 10' onwards are easy to refute.

Dias 5 & 6 - Back to after Dia 2.

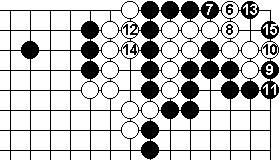
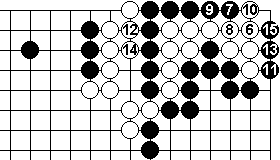
The other two possible moves for White 6 are easily countered.

I conclude that Black can kill White.

An Ishi format file of these investigations is available.

Home > Steve > Go > Problem of the month
British Go Association
Last updated 2004-08-10
This page is part of http://www.stocton.org/
Email: webmaster@stocton.org